周波数カウンタ組立キット
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
たまにはちょいと息抜きで小品も作ってみたいものです。
簡単にチョイチョイと…。
でも、なかなかそうは簡単にはいかなくて、いつものごとく回を重ねてしまうことになるのかも…。
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜
[第46回]
●計算が合いません?(2)
前回の訂正です。
前回の割込みプログラムの計算にミスがありました。
割込みプログラムの実行時間は3.9μsと書きましたが3.6μsの間違いでした。
本日になりましてから正しい計算式の説明を書こうとしましたら、計算の結果が合いません。
前回アドレス0004のGOTO命令を計算に入れてなかったことに気が付いてそれを加算したのですが、そのために結果が食い違ってきてしまいました。
しかしそのGOTO分のクロック数を加算すること自体は必要です。
するとどこか誤って多く加算しているところがあるはず、と思ってよくよく考えてみましたら、割込み遅延のクロック数を取り違えていました。
お恥ずかしい次第です。
前回引用したData Sheetのタイミングチャートで割込み遅延(interrupt latency)が3−4命令クロックとあるところをそのまま鵜呑みにして割込みプログラムに3.5クロックを加算してしまいました。
interrupt latencyは割込み信号が受け付けられてから実際に割込みプログラムが実行されるまでの遅延時間で、割込みプログラムの実行時間に加えるべきものではありませんでした。
実際に割込みによって余分に挿入される命令時間はそのタイミングチャートでDummy Cycleと書いてある2命令クロックでした。
したがって(アドレス0004のGOTO命令を含めて)割込みプログラム自体に加算すべきクロック数はそのDummy Cycleの2クロックです。
あらためてそれを計算すると、0004のGOTO(2)+INT(14)+Dummy Cycle(2)=18クロックになります。
1命令クロックは20MHzの場合0.2μsですから、割込みプログラムの実行時間は3.6μsになります。
なお前回の該当部分は訂正済みです。
さてあらためて前回の要約です。
テストに使ったPICプログラムのカウントデータ表示間隔は実測値では割込みが無いときは66秒で、割込みが入ると80秒でした。
12.8MHzをカウントしているとき、割込みは20μsごとに入り、割込みプログラムの実行時間は3.6μsです。
つまり通常は実行時間が20μsのところが割込みが入ると1.18倍の23.6μsになります。
そこで65.5×1.18=77.29と計算しましたが80秒には届きません。
66×1.18=77.88でも同じです。
なぜ計算が合わないのでしょうか?
というところで前回は終りました。
上の計算は割込みによって増加した時間にも割込みが入る、ということを考慮に入れていませんでした。
しかしそれを考慮した計算はどのようにすればよいのでしょうか?
なんだか複雑な数式になりそうです。
こういうときは簡単な例で考えてみると計算のヒントが求まったります。
小学校の算数の考え方ですが、これが意外に役立ちます。
仮に割込み無しのときに実行時間が200μsであるようなプログラムを考えてみます。
割り込みは20μsごとに入り、割込みプログラムの実行時間は3μsです。
このときの全体の実行時間を図で求めてみます。
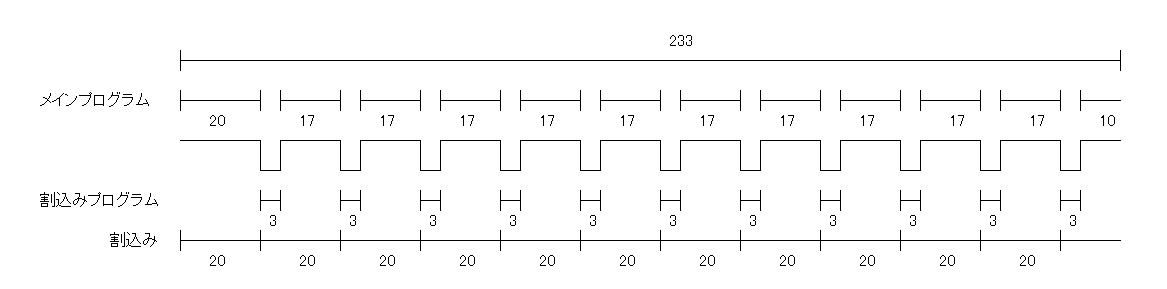
おお、計算のヒントがみつかりました。
メインプログラムは割込みプログラムが実行されている間待たされますから、次の割込みまでの間に実行できるのは割込み間隔−割込みプログラムの実行時間です。
ここから割込み回数が求まります。
求めた割込み回数に割込み間隔を掛ければ解が求まります。
前後に端数がありますから概算になりますが今回の目的にはこれで十分です。
さっそくやってみましょう。
まず割込み回数を求めます。
N=66000/(0.02−0.0036)
=66000/0.0164
=4024390
求めたNに割込み間隔を掛ければ解が求まります。
T=0.02*N
=0.02*4024390
=80487.8
80秒が求まりました。
これにて一件落着です。
周波数カウンタ組立キット[第46回]
2015.11.6upload
前へ
次へ
ホームページトップへ戻る