超巨大基板の8080互換HCMOS・CPUでCP/Mを走らせてしまおうという、なんとも狂気なプロジェクトです!
[第58回]
●なぜ最良近似式か?
このところずっと「最良近似式」について書いております。
しかし、そもそも一体なぜ「最良近似式」なのでありましょうか?
通常の「近似式」と「最良近似式」とは一体どこが違うのでありましょうか?
そこのところで得心がいきませんと、何をやっているのやらさっぱりわからぬ、ということになってしまいます。
ですので、まずはそのあたりについて、簡単に見ていただくことにいたします。
下のグラフは前回も見ていただきましたsin(x)をf(x)としたときの、その近似式g(x)との差
E(x)=f(x)−g(x)
のグラフです。
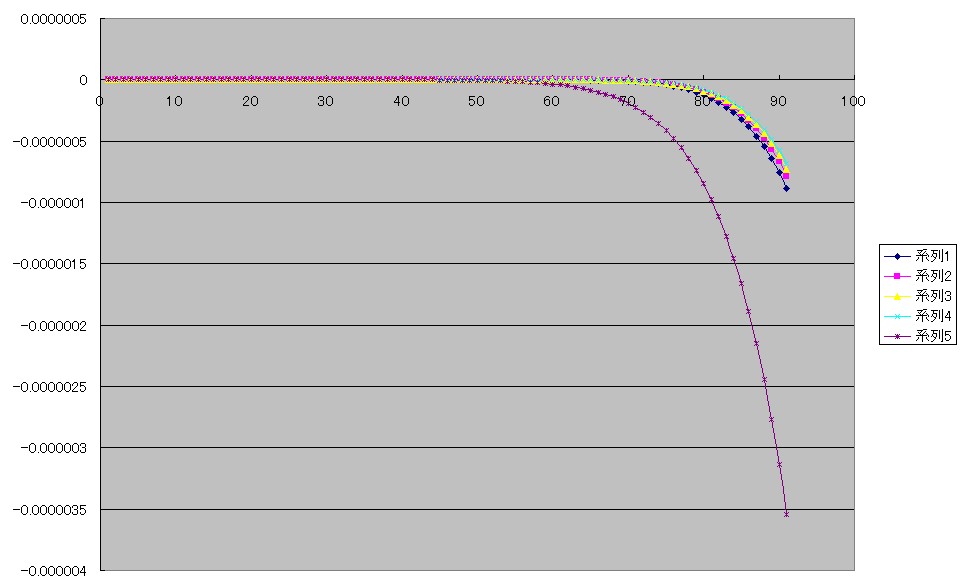
しかし前回とは違い、今回は最良近似式ではなくてただの近似式のグラフです。
系列1はチェビシェフの9次の近似式(下の式)の誤差のグラフです。
sin(x)=c1x+c3x3+…+c9x9
c1=1
c3=−0.166666661
c5=0.008333303
c7=−0.000198344
c9=2.68684×10−6
系列2、系列3、系列4は上記のチェビシェフの近似式をもとにして最良近似式を導き出す途中の近似式です。
そして系列5はテイラーの9次の多項式(下の式)です。
sin(x)=c1x+c3x3+…+c9x9
c1=1
c3=1/3!=1/6
c5=1/5!=1/120
c7=1/7!=1/5040
c9=1/9!=1/362880
上のグラフを見ますとテイラーの式は60°近くまでは誤差はほとんど無いように見えますが、60°を越えるあたりから誤差が急に大きくなっています。
前回の最良近似式との違いはまさにその点にあります。
テイラーの多項式でこの誤差を小さくするためにはひたすらxの次数の大きな項まで計算するしかありません。
そのようにしても90°近くの誤差はなかなか小さくはできませんが、計算量は飛躍的に増大してしまいます。
下は上のグラフを60°近くまでで止めたものです。
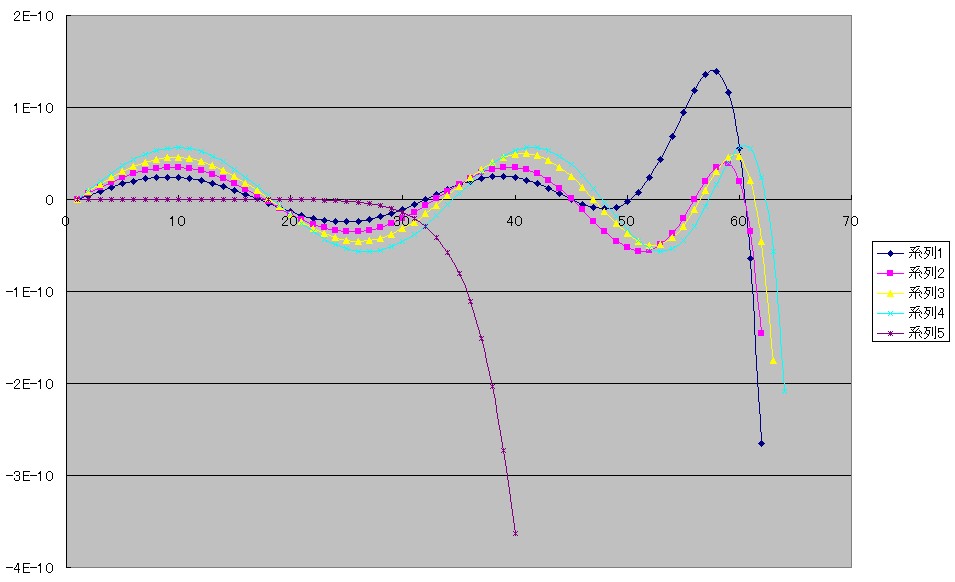
テイラーの多項式のグラフ(系列5)はさきほどのグラフでは60°近くまでは誤差が小さいように見えたのですが、このように拡大してみますと、もっと早く30°を越えるあたりから誤差が急に増大していることがわかります。
0°から90°までの全範囲にわたってある一定以下の誤差範囲で使いたいと考えたとき、テイラーの式は使えないなあ、ということがおわかりいただけると思います。
チェビシェフの近似式(系列1)は60°近くまでは誤差を一定範囲に押さえようとしているように見えますが、それを越えるとやはり誤差が急に大きくなってしまいます。
チェビシェフの近似式は「最良近似式」ではない、と評される所以です。
本日は時間がなくなってしまいました。
次回に続きます。
MYCPU80でCP/Mを![第58回]
2014.10.29upload
前へ
次へ
ホームページトップへ戻る